4D SDFs: Building 4D Shapes with Ray Marching

Ray Marching

Ray marching is the process of casting a ray in the direction of a pixel, calculating the distance to the nearest surface, and marching forward. By calculating the distance to the nearest surface, and using some extra logic, each pixel of an image can be coloured according to the scene defined by a signed distance function.

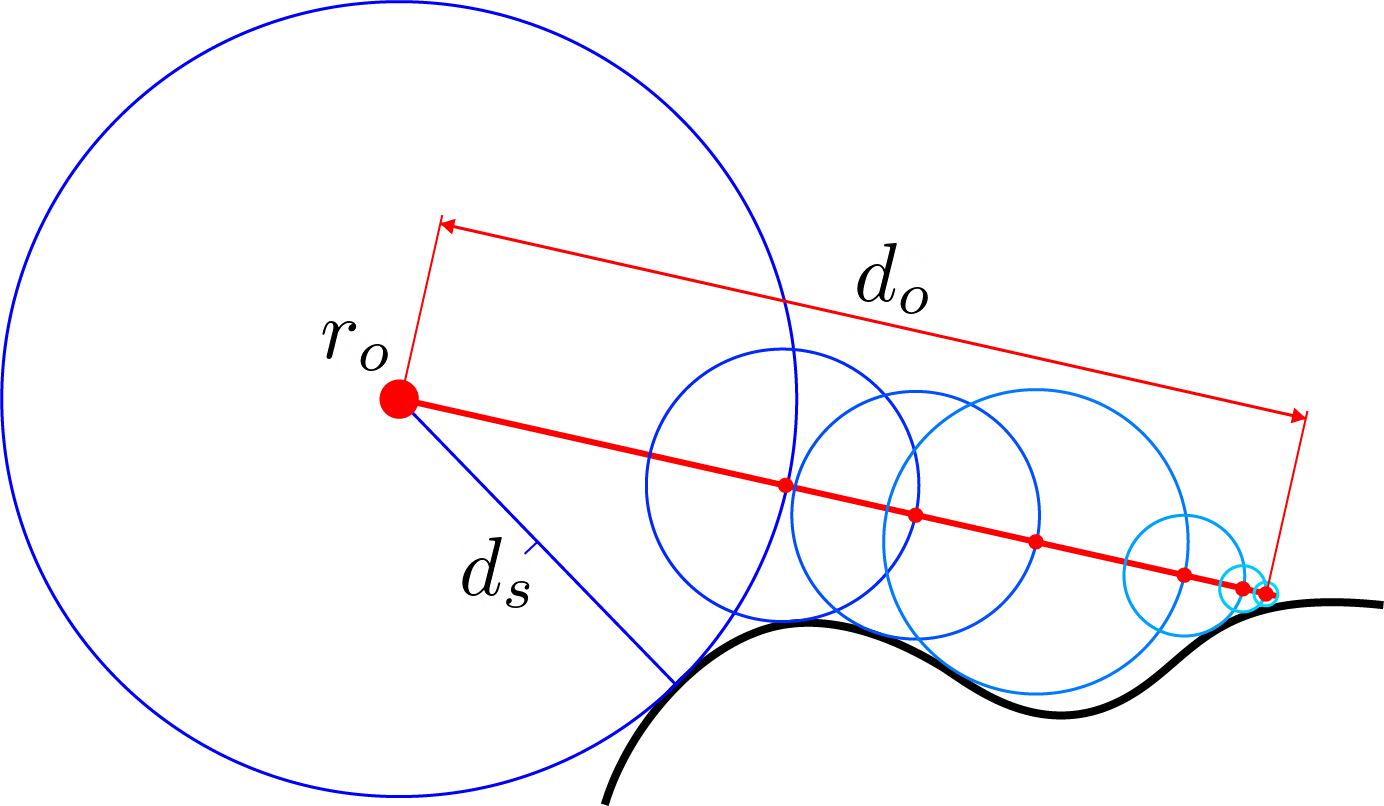
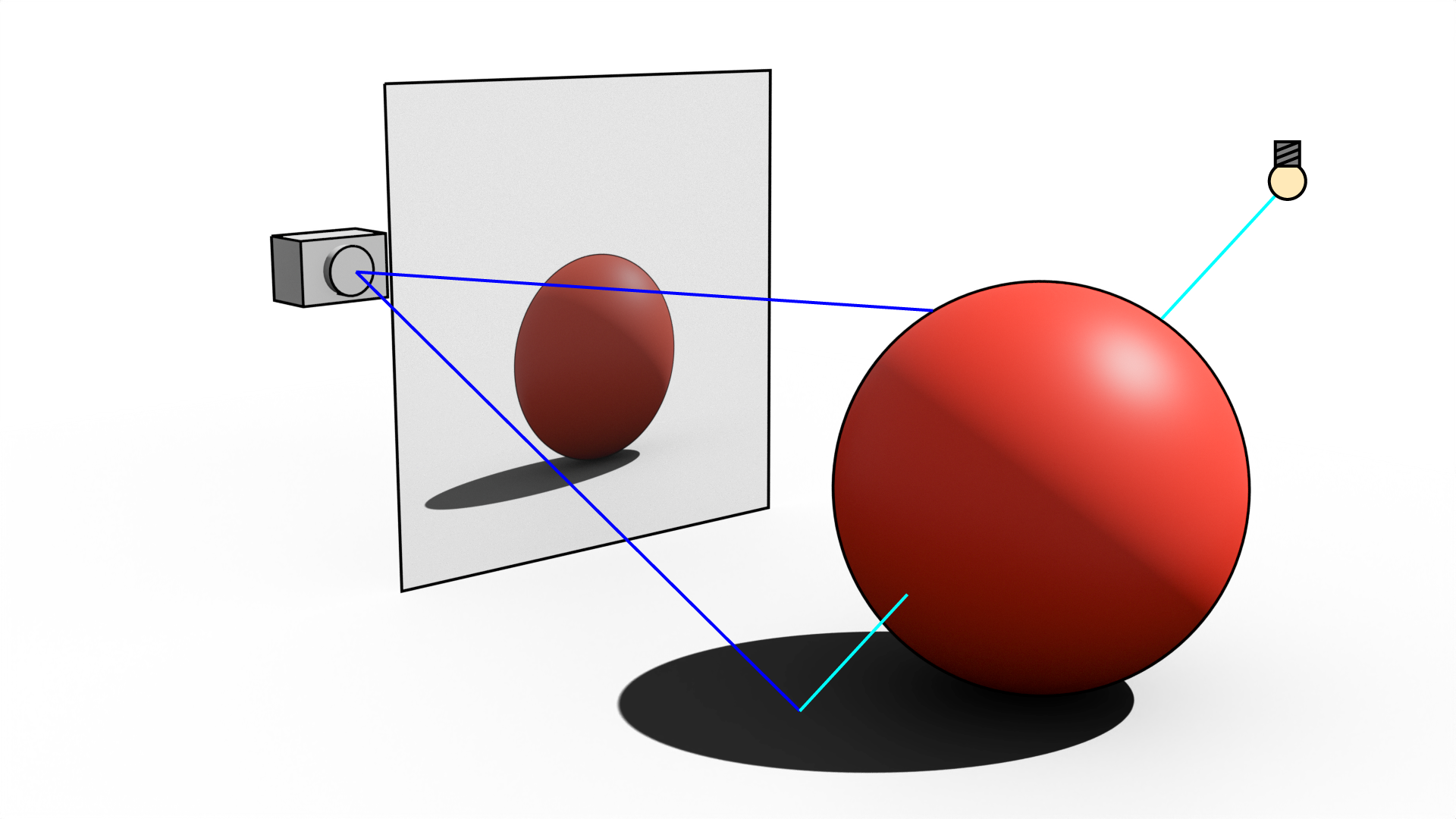
For more information on ray marching, check out The Art of Code on youtube, and Inigo Quilez's blog covering a huge range of SDFs and other functions used in ray marching.

Signed Distance Functions (SDFs) for 4D Shapes

Check out my 4D SDFs written in HLSL here.

Sphere

A sphere is defined purely by a radius subtracted from its origin point

float sdSphere(float4 p, float r)
{
    float d = length(p) - r;
    return d;
}

Box

The box is defined by its hight/width along each of the 4D axes. This SDF does not utilise an interior distance, and therefore can occasionally produce a glitchy surface. This can be avoided by giving the box thickness by subtracting a small value. Note: subtracting larger values will produce rounded edges.

float sdBox(float4 p, float4 s)
{
    float d = length(max(abs(p) - s, 0));
    return d;
}

Torus (2 Radii)

A torus with with two radii, \(r1\) and \(r2\), defines a circular path with radius \(r1\), with a thickness in all dimensions defined by radius \(r2\). The cross section of this may appear as two spheres

float sdTorus(float4 p, float r1, float r2)
{
    float d = length(
                float2(
                    length( 
                    float2(length(p.zx) - r1, p.y)
                            ), p.w
                    )) - r2;
    return d;
}

Torus (3 Radii)

A torus with with three radii \(r1\), \(r2\) and \(r3\), defines a major circular path with radius \(r1\). A second minor circular path defined by \(r2\) follows the major path. This minor path is then given a thickness defined by radius \(r3\). The cross section of this may appear as two tori.

float sdTorus(float4 p, float r1, float r2, float r3)
{
    float d = length(
                float2(
                    length( 
                    float2(length(p.zx) - r1, p.y)
                            ) - r2, p.w
                    )) - r3;
    return d;
}

Cone (Extended along w)

The surface of the cone is calculated as a function of its height and radius at the base of the cone.

float sdConeW(float4 p, float r, float h)
{
    float2 q = float2(length(p.xyz), p.w);
    float2 tip = q - float2(0, h);
    float2 mantleDir = normalize(float2(h, r));
    float mantle = dot(tip, mantleDir);
    float d = max(mantle, -q.y);
    float projected = dot(tip, float2(mantleDir.y, -mantleDir.x));

    // distance to tip
    if ((q.y > h) && (projected < 0)) {
        d = max(d, length(tip));
    }

    // distance to base ring
    if ((q.x > r) && (projected > length(float2(h, r)))) {
        d = max(d, length(q - float2(r, 0)));
    }
    return d;
}

Capsule

A capsule is defined as the path between two points; \(a\) and \(b\). This path is then given thickness. The capsule can be plotted manually, or a helper function can be defined for simpler use in code.

float sdCapsule( float4 p, float4 a, float4 b, float r )
{
    float4 pa = p - a, ba = b - a;
    float h = clamp( dot(pa,ba)/dot(ba,ba), 0.0, 1.0 );
    return length( pa - ba*h ) - r;
}

float sdCapsuleW(float4 p, float length, float r)
{
    float l = length/2;

    return sdCapsule(p, 
                     float4(0, 0, 0,-l),
                     float4(0, 0, 0, l),
                     r
                    );
}

Pentachoron (Hyper Tetrahedron)

A plane is defined at each vertex of the pentachoron, and the boolean intersection of all these planes is accumulated. This produces a hyper tetrahedron which can be scaled using the parameter \(s\), in the same way a sphere is defined by subtracting the radius.

float sdPentachoron(float4 p, float s){
    float a = +p.x +p.y -p.z -p.w;
    float b = -p.x -p.y -p.z -p.w;
    float c = +p.x -p.y +p.z -p.w;
    float d = -p.x +p.y +p.z -p.w;
    float e = p.w;
    return (max(max(max(a,b),max(c,d)), e)-s)/sqrt(5.);
}